With the rise of functional programming in Javascript, it’s increasingly likely that you’ll have come across, or written recursive functions. They allow us to express the solution to a big problem in terms of solving “this one step, plus the solution to the rest”.

If we express that in a more functional notation, it’s akin to fn(x :: xs) = x + fn(xs). This post serves to warn about the limitations of this type of function, and to suggest an alternative for when the situation requires us to exceed those limitations.

This topic came up as part of optimizing tree traversal methods, but for simplicity we will use sum for the examples. The learnings should apply equally to any type of recursive problem, although the runtime constants/impact will vary. Since sum is a single subproblem recursion, we also include treeSum examples for how to handle multiple recursion.

Recursive functions and the call stack

Say we want to express the sum of a list of numbers, we can express it as the value of the first element, plus the sum of the rest: list[0] + sum(list.slice(1)). We also need to handle the empty list, to create our base case and avoid infinite recursion. Expressed as a ternary (inline if statement), this becomes:

const sum = list => (list.length ? list[0] + sum(list.slice(1)) : 0);

If we try it out with a small list of numbers, everything looks fine.

sum([1, 1, 2, 2]); // 6

If suddenly the guy producing the numbers had a really productive day, and gave us a list of 1.000.000 numbers, we have a problem:

// create list of one million 1s:
const oneMillionInSingles = Array.from(new Array(1000000), () => 1);
sum(oneMillionInSingles);
// Uncaught RangeError: Maximum call stack size exceeded

It comes down to the call stack, since every time we call a function, the engine needs to keep track of where we were, so it can resume from there when the function returns. By doing this in a way that is dependent on the input size, we naturally limit how big problems we can solve with that function without encountering the infamous Uncaught RangeError: Maximum call stack size exceeded.

The limit might vary depending on the engine, browser, node version, but we should be grateful that it’s trying to save us from what is by any reasonable measure, an infinite recursion.

So how can we handle bigger inputs without blowing the stack?

Beating the stack limit with a loop

What if we just used a loop? I know, I know, we will lose all those cool points, and our street cred might never fully recover. But sometimes it’s better to be correct than cool. Stay with me.

The sum function can be written with a loop.

const boringSum = list => {
	let acc = 0;
	for (let i = 0; i < list.length; i++) {
		acc += list[i];
	}
	return acc;
};

boringSum can handle our million dollars in singles just fine. It’s a better solution to the problem, even if it’s not as elegant.

It also comes with a significant performance boost, since we are not creating all those stack frames, and can sometimes make the difference between a solution that is too slow, and one that is fast enough™.

Sidenote: while the sum function would probably be best done as a reducer function, this does not generalize well to cases where the solution calls for multiple subproblem recursion. E.g. for traversing a tree, we will want to process the current node, and add all the children to the stack/queue. In a binary tree, summing over the nodes looks something like this.

// Recursive tree depth first tree sum:
const binaryTreeSum = root =>
	root ? root.value + binaryTreeSum(root.left) + binaryTreeSum(root.right) : 0;
const naryTreeSum = root =>
	root.value + root.children.reduce((acc, child) => acc + naryTreeSum(child), 0);

// Loop based depth first tree sum:
const boringTreeSum = root => {
	let acc = 0;
	const nodes = [root];
	while (nodes.length) {
		// Use .pop instead of shift for Breadth first traversal
		const node = nodes.shift();

		acc += node.value;
		// binary case:
		if (node.left) nodes.push(node.left);
		if (node.right) nodes.push(node.right);
		// n-ary case:
		// nodes = nodes.concat(node.children);
	}
	return acc;
};

Tail call optimization

Rewriting recursion into a loop is basically what the compiler will do in languages that have proper tail call optimization. But only if the code is written in a form that allows it.

The rule of thumb is that if the expressions in the current scope cannot be evaluated before recursing, the compiler cannot help you.

Consider it equivalent to either evaluating 1 + (2 + (3 + (4))) or 1 + 2 + 3 + 4. For 1 + (2 + (3 + (4))), we first encounter 1 + (...), and we make a note of that. To continue we evaluate 2 + (...), but need first evaluate the second part, etc. On the other hand, 1 + 2 + 3 + 4 can be collapsed immediately when we see 1 + 2, to 3 + 3 + 4, without making any notes and partial results. If you’ve ever used a calculator with Reverse Polish Notation, you will be familiar with the cumbersome process of calculating the first example instead of the second, since each paren requires another number to be pushed onto the stack.

In practice, this is commonly solved by introducing an accumulator. Basically we keep a running sum, such that instead of creating a call stack with sum([1, 2, 3, 4]) of 1 + (2 + (...)) we can evaluate the plus immediately, and pass it on to a new function call as the accumulator argument.

This allows the runtime to swap the current stack frame with the new function call, i.e. ‘not to take notes’. There is no longer a need to remember every previous frame in order to get the final result.

const tailcallSum = (list, acc = 0) => (list.length ? sum(list.slice(1), list[0] + acc) : acc);

But… NodeJS had tail call optimization for a while (v6.2 to v7.10), but due to limitations in the underlying V8 engine, it is no longer available.

The support in your favorite browser might already be here, but support is very sparse. Consider it future proofing, or a way of opting into a future performance boost. Who can say no to that?

Benchmarks

This is a classic case of don’t do this at home. Or don’t base your decisions on micro benchmarks, since a real world use case will involve all kinds of compiler magic, that might interfere with the characteristics of a small snippet of code, in order to better optimize on a higher level, or because the optimizing compiler has deoptimized your code due to exceptions.

With those disclaimers out of the way, let’s look at the numbers from running some Recursion microbenchmarks

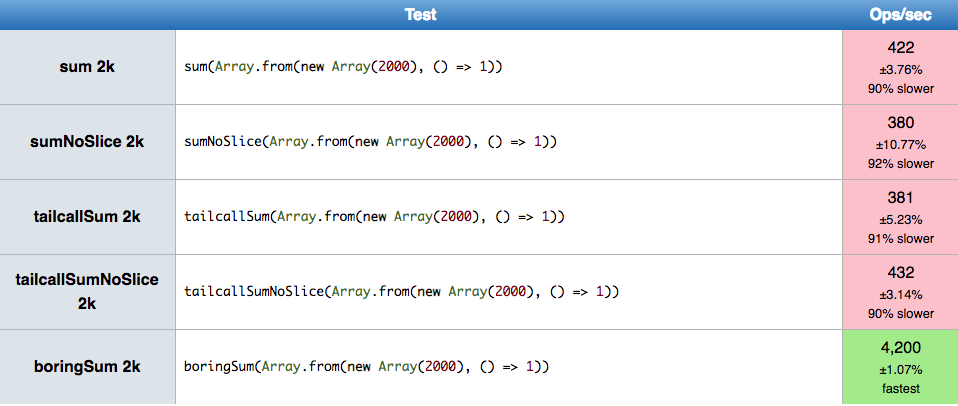
Even though it will vary per browser, the conclusion is pretty clear. A simple loop is a lot more efficient than any of the recursive forms.

We can even see it visually, how they affect the call stack, by using devtools to run a performance profile. The flame chart for the recursive sum shows the deep call stack very clearly:

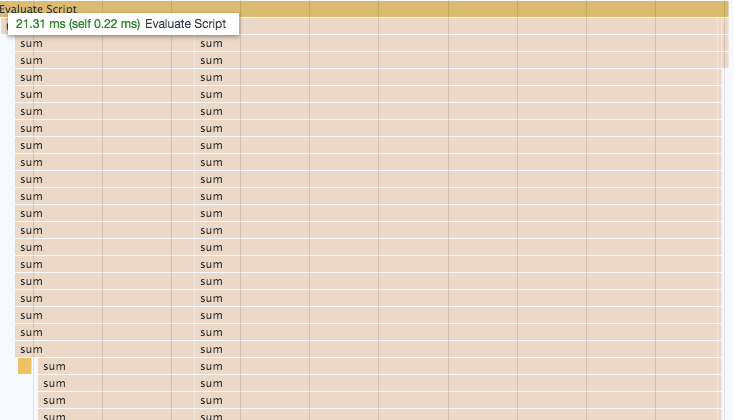
The same graph for the loop based function is hardly doing any work in comparison:

By this very small sample size, we can expect a 10x (chrome) to 100x (safari) speedup, with inputs causing 2k recursion depths.

Conclusion

The support for optimized recursion in Javascript is still quite limited. As long as that’s the case, we have to approach it with caution, and be ready to consider the alternatives.

Definitely think twice about using recursive definitions for bigger problems. If you are writing performance critical code, refactoring a hot code path, or trying to optimize the startup of your apps, rewriting a recursive function to a simple loop might be an easy win!

Posted in Programming